LAS MEDIDAS DE DISPERSIÓN SON VALORES NUMÉRICOS QUE MIDEN LA DISPERSIÓN O VARIABILIDAD ENTRE LOS DATOS.
ES DECIR, SI LOS DATOS ESTÁN CERCA O PRÓXIMOS AL PROMEDIO, CON RESPECTO A LA ESCALA EN LA CUAL SE MIDIERON , LAS MEDIDAS DE DISPERSIÓN TOMAN VALORES PEQUEÑOS.
SI POR EL CONTRARIO, LOS DATOS ESTÁN RELATIVAMENTE LEJANOS DEL PROMEDIO, LAS MEDIDAS DE DISPERSIÓN TOMARÁN VALORES NUMÉRICOS GRANDES.
LAS PRINCIPALES MEDIDAS DE DISPERSIÓN SON LA VARIANZA LA DESVIACIÓN TÍPICA Y LA DESVIACIÓN ESTÁNDAR
VARIANZA
LA VARIANZA ES UNA MEDIDA QUE PRETENDE ESTABLECER LA CERCANÍA DE CADA UNO DE LOS DATOS CON RESPECTO DE LA MEDIA. PARA CALCULAR LA VARIANZA ES NECESARIO DETERMINAR LA DISTANCIA DE CADA UNO DE LOS DATOS A LA MEDIA. PARA ELLO TENEMOS LAS FÓRMULAS
CUANDO SE CUENTA CON TODOS LOS DATOS SE USA LA POBLACIONAL
CUANDO NO SE CUENTAN CON TODOS LOS DATOS DE LA POBLACIÓN SE USA LA MUESTRAL.
EJEMPLO
SE DESEA CALCULAR LA VARIANZA (POBLACIONAL Y MUESTRAL) DE UNOS DATOS, TOMANDO COMO REFERENCIA LAS EDADES DE 20 ASPIRANTES A MAQUILLADORES PARA UNA PELÍCULA. ESTOS DATOS SON:
ES DECIR, SI LOS DATOS ESTÁN CERCA O PRÓXIMOS AL PROMEDIO, CON RESPECTO A LA ESCALA EN LA CUAL SE MIDIERON , LAS MEDIDAS DE DISPERSIÓN TOMAN VALORES PEQUEÑOS.
SI POR EL CONTRARIO, LOS DATOS ESTÁN RELATIVAMENTE LEJANOS DEL PROMEDIO, LAS MEDIDAS DE DISPERSIÓN TOMARÁN VALORES NUMÉRICOS GRANDES.
LAS PRINCIPALES MEDIDAS DE DISPERSIÓN SON LA VARIANZA LA DESVIACIÓN TÍPICA Y LA DESVIACIÓN ESTÁNDAR
VARIANZA
LA VARIANZA ES UNA MEDIDA QUE PRETENDE ESTABLECER LA CERCANÍA DE CADA UNO DE LOS DATOS CON RESPECTO DE LA MEDIA. PARA CALCULAR LA VARIANZA ES NECESARIO DETERMINAR LA DISTANCIA DE CADA UNO DE LOS DATOS A LA MEDIA. PARA ELLO TENEMOS LAS FÓRMULAS
CUANDO SE CUENTA CON TODOS LOS DATOS SE USA LA POBLACIONAL
CUANDO NO SE CUENTAN CON TODOS LOS DATOS DE LA POBLACIÓN SE USA LA MUESTRAL.
EJEMPLO
SE DESEA CALCULAR LA VARIANZA (POBLACIONAL Y MUESTRAL) DE UNOS DATOS, TOMANDO COMO REFERENCIA LAS EDADES DE 20 ASPIRANTES A MAQUILLADORES PARA UNA PELÍCULA. ESTOS DATOS SON:
35,32,28,28,35,30,32,31,29,27,33,25,32,33,28,42,40,39,41,40
SOLUCIÓN 1
PARA CALCULAR LA VARIANZA POBLACIONAL SE DEBEN REALIZAR LOS SIGUIENTES 2 PASOS:
1. CALCULAR PROMEDIO (sumar todos los datos y dividirlos entre la cantidad de datos)
SOLUCIÓN 2
1. CALCULAR PROMEDIO (sumar todos los datos y dividirlos entre la cantidad de datos)
2. REALIZAR LA SUMATORIA DE LAS RESTAS DE CADA UNO DE LOS DATOS CON EL PROMEDIO Y EL RESULTADO ELEVÁNDOLO AL CUADRADO.
PARA CALCULAR LA VARIANZA MUESTRAL DE LOS DATOS SE DEBEN REALIZAR LOS SIGUIENTES 3 PASOS:
1. CALCULAR PROMEDIO (sumar todos los datos y dividirlos entre la cantidad de datos)
VP= 37.75 VM= 39.73
DESVIACIÓN ESTÁNDAR O TÍPICA
LA DESVIACIÓN ESTÁNDAR O TÍPICA, ES LA RAÍZ CUADRADA POSITIVA DE LA VARIANZA.
1. CALCULAR PROMEDIO (sumar todos los datos y dividirlos entre la cantidad de datos)
2. REALIZAR TABLA CON LOS DATOS, SUS CUADRADOS Y LAS RESPECTIVAS SUMATORIAS
3. SUSTITUIMOS EN LA FÓRMULA, LOS VALORES QUE SE ACABAN DE OBTENER Y SE REALIZAN CÁLCULOS
CONCLUSIÓN:
COMO LA RESPUESTA ES UN NÚMERO "ALTO" QUIERE DECIR QUE LOS DATOS ESTÁN ALEJADOS DEL PROMEDIO. ES DECIR GRUPO CON DATOS DISPERSOS, COMO LO PODEMOS APRECIAR EN EL SIGUIENTE GRÁFICO
PRÁCTICA 1:
CALCULAR LA VARIANZA POBLACIONAL Y MUESTRAL DE LOS SIGUIENTES DATOS
55,78,50,41,55,35,41,42,51,54,41,54,72,76,75,47,62,59,75,46
promedio=55.45 vp=173.2475 vm=182.36
PRÁCTICA 2:
UN GALPÓN DESEA SABER SI LA REGULARIDAD DE LA PRODUCCIÓN DE HUEVOS ES HOMOGÉNEA (CONSTANTE) Y PARA ESTO LLEVA EL REGISTRO DE LA PRODUCCIÓN DURANTE 14 DÍAS, TENIENDO LOS SIGUIENTES RESULTADOS
150, 245,200,225,301,185,207,217,350,305,280,310,200,185
a. CALCULAR LA VARIANZA POBLACIONAL 3268.85
b. CALCULAR LA VARIANZA MUESTRAL 3520.307
PRÁCTICA 3:
CALCULAR LA VARIANZA POBLACIONAL Y MUESTRAL A PARTIR DE LA GRÁFICA.
DESVIACIÓN ESTÁNDAR O TÍPICA
LA DESVIACIÓN ESTÁNDAR O TÍPICA, ES LA RAÍZ CUADRADA POSITIVA DE LA VARIANZA.
EJEMPLO
EL DEPARTAMENTO DE CONTROL DE CALIDAD DE UNA EMPRESA DE ENSAMBLAJE DE MOTOCICLETAS TOMÓ UNA MUESTRA DE 16 DE SUS VEHÍCULOS PARA DETERMINAR LA DISTANCIA QUE RECORRE CADA MOTO CON UN GALÓN DE GASOLINA. LOS RESULTADOS FUERON:
115,125,143,117,136,144,112,128,151,139,154,126,140,140,145,155
CALCULAR LA DESVIACIÓN ESTÁNDAR POBLACIONAL Y MUESTRAL
SOLUCIÓN
PARA CLACULAR ESTA DESVIACIÓN POBLACIONAL SE DEBEN REALIZAR LOS SIGUIENTES 3 PASOS:
1. CALCULAR PROMEDIO
3. SE CALCULA LA DESVIACIÓN POBLACIONAL. (sacarle la raíz cuadarada a la varianza poblacional)
DESVIACIÓN MEDIA
LA DESVIACIÓN MEDIA ES EL PROMEDIO DE LA SUMATORIA DE LAS RESTAS DE LOS DATOS CON EL PROMEDIO DE LOS DATOS. SE RESUME EN LA SIGUIENTE FÓRMULA
PARA CALCULAR ESTA DESVIACIÓN MUESTRAL SE DEBEN REALIZAR LOS SIGUIENTES 3 PASOS:
1. SE CALCULA LA VARIANZA MUESTRAL.
5. SE CALCULA LA DESVIACIÓN MUESTRAL. (sacarle la raíz cuadrada a la varianza muestral)
PRÁCTICA 1
CALCULAR LA DESVIACIÓN ESTÁNDAR (POBLACIONAL Y MUESTRAL) DE LOS SIGUIENTES DATOS
380,400,300,389,310,320,361,390,305,369,390,301,353,405,360,302,348,345,351,352
DP=34.24 DM=35.13
PRÁCTICA 2
DE UN GRUPO DE 30 PERSONAS SE HA RECOLECTADO LA INFORMACIÓN DEL PESO DE 20 DE ELLAS OBTENIENDO LOS SIGUIENTES RESULTADOS
84kg, 62kg, 55kg, 40kg, 73kg, 60Kkg, 68kg, 68kg, 72kg, 61kg, 63kg, 79kg, 55kg, 58kg, 76kg, 67kg, 57kg, 70kg,82kg, 58kg
CALCULAR LA DESVIACIÓN MÁS APROPIADA Y DETERMINAR SI HAY SOBREPESO EN EL GRUPO Y SI LOS DATOS SON HOMOGÉNEOS
Rta= 10.67
PRÁCTICA 3
A PARTIR DE LA GRÁFICA CALCULAR LA DESVIACIÓN ESTÁNDAR POBLACIONAL Y MUESTRAL Y DETERMINAR SI EL GRUPO ES O NO HOMOGÉNEO
DESVIACIÓN MEDIA
LA DESVIACIÓN MEDIA ES EL PROMEDIO DE LA SUMATORIA DE LAS RESTAS DE LOS DATOS CON EL PROMEDIO DE LOS DATOS. SE RESUME EN LA SIGUIENTE FÓRMULA
EJEMPLO
CALCULAR LA DESVIACIÓN MEDIA DE LOS SIGUIENTES DATOS:
55,45,56,74,80,70,67,63,49,51
SOLUCIÓN
1. SE CALCULA EL PROMEDIO
2. SE REALIZA LA SUMATORIA Y SE DIVIDE ENTRE LA CANTIDAD DE DATOS
PRÁCTICA 1
CALCULAR LA DESVIACIÓN MEDIA DE LOS SIGUIENTES DATOS
155,165,167,175,145,153,158,163,180,167
PRÁCTICA 2
8,6,7,9,9,1,10,12,12,15,15,18,19,11,17
CALCULAR LA DESVIACIÓN MEDIA DE LOS SIGUIENTES DATOS
PRÁCTICA 3
CALCULAR LA DESVIACIÓN MEDIA A PARTIR DE LA SIGUIENTE GRÁFICA
Dm= 8.46
CALCULAR LA DESVIACIÓN MEDIA DE LOS SIGUIENTES DATOS:
55,45,56,74,80,70,67,63,49,51
SOLUCIÓN
1. SE CALCULA EL PROMEDIO
2. SE REALIZA LA SUMATORIA Y SE DIVIDE ENTRE LA CANTIDAD DE DATOS
PRÁCTICA 1
CALCULAR LA DESVIACIÓN MEDIA DE LOS SIGUIENTES DATOS
155,165,167,175,145,153,158,163,180,167
PRÁCTICA 2
8,6,7,9,9,1,10,12,12,15,15,18,19,11,17
CALCULAR LA DESVIACIÓN MEDIA DE LOS SIGUIENTES DATOS
PRÁCTICA 3
CALCULAR LA DESVIACIÓN MEDIA A PARTIR DE LA SIGUIENTE GRÁFICA
Dm= 8.46









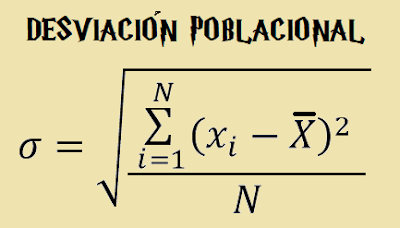












Buenas tardes profesor, me preguntaba cuáles son los ejercicios que hay que realizar ya que los que están acá tienen las respuestas.
ResponderEliminarbuenos días profesor yo tampoco encuentro los ejercicios que hay que realizar soy Daniel perez del 902
ResponderEliminarbuenas tardes profesor, me preguntaba cuando va hacer la conferencia para esplicar eso
ResponderEliminarBuenos tardes profesor, revise y no encuentro los ejercicios que hay que hacer.
ResponderEliminar